熱線電話:0755-23712116
郵箱:contact@shuangyi-tech.com
地址:深圳市寶安區沙井街道后亭茅洲山工業園工業大廈全至科技創新園科創大廈2層2A

3D坐標繞軸旋轉公式推導
繞軸旋轉實際上等價于平面點繞遠點旋轉,所以這里只用分析一下平面情況就可以。
問題轉換為:平面上任意點(x,y)繞原點旋轉R度后,新點坐標為多少?
一、通常情況,我們容易想到一下的推導方式(我一開始想到的),請看下圖:
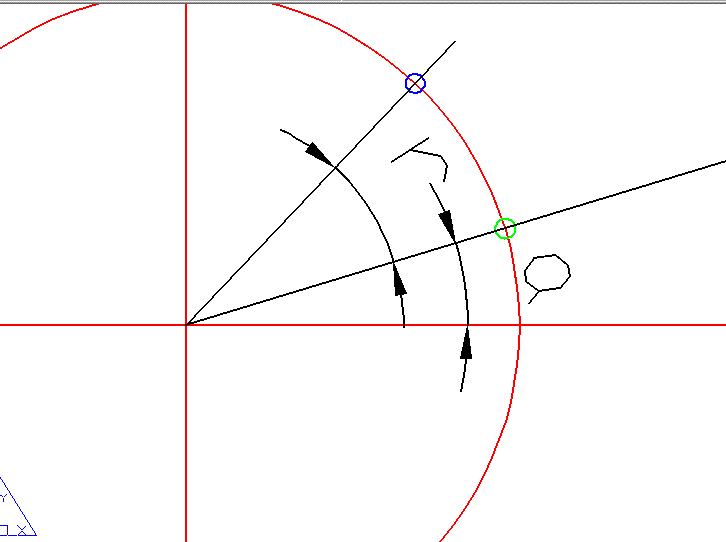
綠色的點為原始點(x,y),轉過r度后到藍色的點的位置,我一開始想到的是先求出初始點(綠色的點)的初始角度a,然后計算出半徑,根據三角關系可以得到新點的坐標。
關系式:
a=arctan(y/x)
radio=sqrt(x*x+y*y)
新點:x’=radio*Cos(a+r); y’=radio*Sin(a+r)
看起來貌似可以,但是編程處理旋轉問題時發現了嚴重的問題,在求a的時候用了x做分母,所以就限定了x不等于0,這就不好了。
二、直角坐標系求解
思考了一天,不知道如何解決分母的問題,突然回想起來以前學過坐標變換,恍然大悟,汗一個。
還是需要通過幾何關系來進行求解,可以避免定義域不連續的問題,無圖無真相!
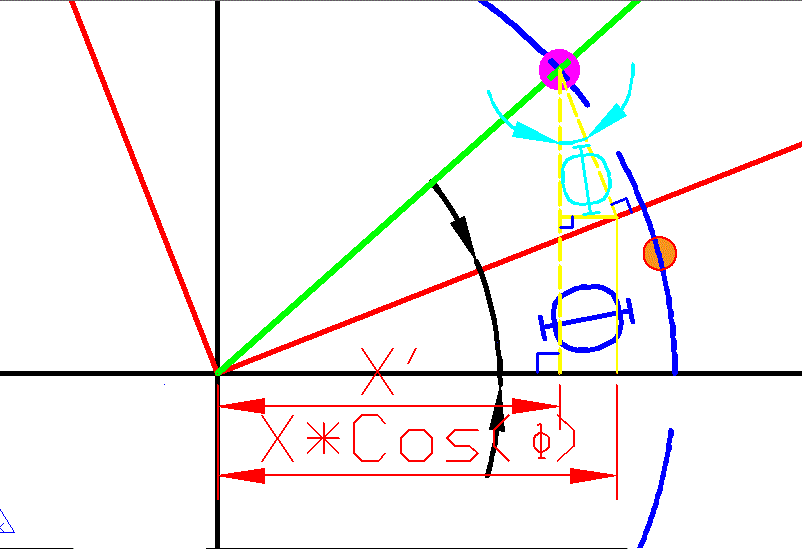
注釋:圖中紅色的點為初始點,粉色的為新點,黑色的線為初始坐標系,紅色的線為假想坐標系,黃色的線都是垂線。
在坐標變換中,我們可以換一種思考方式,點的旋轉實際上可以理解為坐標系旋轉到新的位置,然后求到新點相對于老坐標系的坐標即可。
圖中我們很容易得到標注的兩個角度相等,新點的橫坐標X’等于下面尺寸標注的X*Cos(φ)-兩條黃色的垂線間的距離,而這段距離我們可以在紅色的新坐標系中很容易求出distance=Y * Sin(φ),所以很容易就得到了新點的橫坐標
X’=X*Cos(φ)-Y*Sin(φ) 式①
同理,得到
Y’=X*Sin(φ)+Y*Cos(φ) 式②
式①和式②就是平面任一點繞原點旋轉的方程。
對于3D坐標中,這便是繞Z軸旋轉的公式
X’=X*Cos(φ)-Y*Sin(φ)
Y’=X*Sin(φ)+Y*Cos(φ)
Z’=Z
對于繞其他軸旋轉的公式都可以用此方法得到。
三、
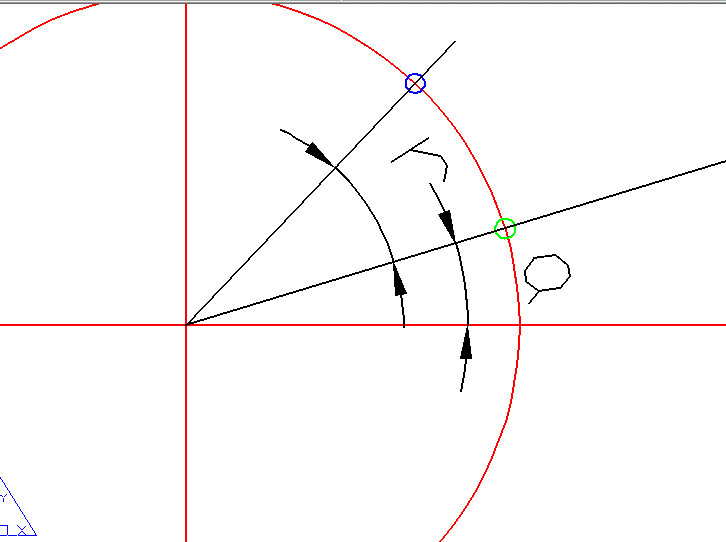
采用三角函數展開將會得到更簡單的求解方法,
X'=Radio*Cos(r+a)
=Radio*(Cos( r)*Cos(a)-Sin( r)*Sin(a))
=Radio*Cos(a)*Cos( r)-Radio*Sin(a)*Sin( r)
=X*Cos( r)-Y*Sin( r)
同理得到
Y’=Radio*Sin(r+a)
=X*Sin( r)+Y*Cos( r)
看來真是要溫故而知新!
坐標旋轉公式
x1=cos(angle)*x-sin(angle)*y;
y1=cos(angle)*y+sin(angle)*x;
其中x,y表示物體相對于旋轉點旋轉angle的角度之前的坐標,x1,y1表示物體旋轉angle后相對于旋轉點的坐標
從數學上來說,此公式可以用來計算某個點繞另外一點旋轉一定角度后的坐標,例如:A(x,y)繞B(a,b)旋轉β度后的位置為C(c,d),則x,y,a,b,β,c,d有如下關系式:
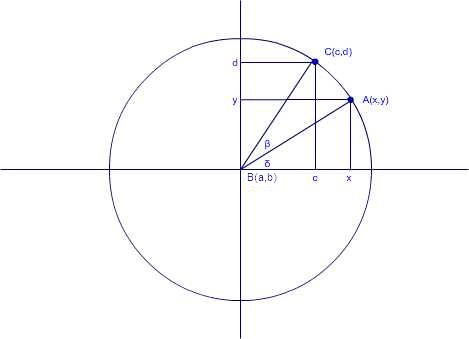
1。設A點旋轉前的角度為δ,則旋轉(逆時針)到C點后角度為δ+β
2。求A,B兩點的距離:dist1=|AB|=y/sin(δ)=x/cos(δ)
3。求C,B兩點的距離:dist2=|CB|=d/sin(δ+β)=c/cos(δ+β)
4。顯然dist1=dist2,設dist1=r所以:
r=x/cos(δ)=y/sin(δ)=d/sin(δ+β)=c/cos(δ+β)
5。由三角函數兩角和差公式知:
sin(δ+β)=sin(δ)cos(β)+cos(δ)sin(β)
cos(δ+β)=cos(δ)cos(β)-sin(δ)sin(β)
所以得出:
c=r*cos(δ+β)=r*cos(δ)cos(β)-r*sin(δ)sin(β)=xcos(β)-ysin(β)
d=r*sin(δ+β)=r*sin(δ)cos(β)+r*cos(δ)sin(β)=ycos(β)+xsin(β)
即旋轉后的坐標c,d只與旋轉前的坐標x,y及旋轉的角度β有關
從圖中可以很容易理解出A點旋轉后的C點總是在圓周上運動,圓周的半徑為|AB|,利用這點就可以使物體繞圓周運動,即旋轉物體。
上面公式是相對于B點坐標來的,也就是假如B點位(0,0)可以這么做。現在給出可以適合任意情況的公式:
x0 = dx * cos(β) - dy * sin(β)
y0 = dy * cos(β) + dx * sin(β)
參數解釋:
x0,y0是旋轉后相對于中心點的坐標,也就是原點的坐標,但不是之前點旋轉后的實際坐標,還要計算一步,
β旋轉角度,可以是順時針或者逆時針。
dx是旋轉前的x坐標-旋轉后的x坐標
dy是旋轉前的y坐標-旋轉后的y坐標
x1=a+x0;
y1=b+y0;
上面才是旋轉后的實際坐標,其中a,b是原點坐標
下面是上面圖的公式解答:
x0=(x-a)*cos(β)-(y-b)*sin(β);
y0=(y-b)*cos(β)+(x-a)*sin(β);
x1=x0+a;
y1=y0+b;